GSoC 2025 - CGAL

CGAL GitHub Issue #9051 - Extending 2D Arrangement Drawings

The 2D Arrangements (Aos2) package in CGAL provides an efficient and extensible framework for representing and manipulating arrangements induced by geometric objects. The existing visualization utilities are useful but exhibit several limitations: inefficient rendering procedures of faces with holes, lack of support for unbounded curves and faces, and inability to correctly render faces on curved surfaces.

This project implements a general renderer for arrangements that integrates with the Aos2 framework and addresses those limitations. The new renderer provides on-demand approximation of x-monotone curves; uses a customized face triangulator to efficiently produce meshes; and leverages tiling and caching to make interactive navigation responsive.

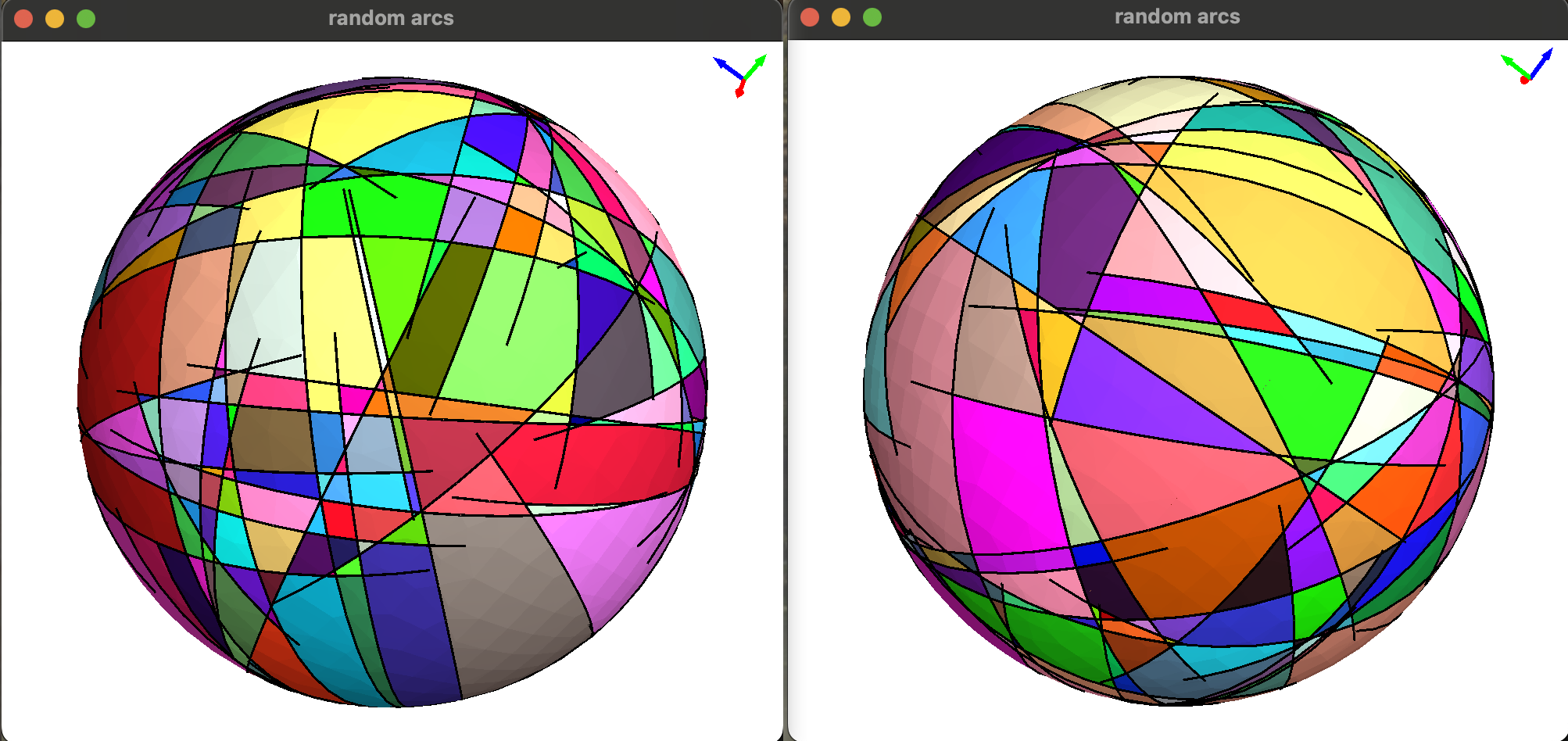
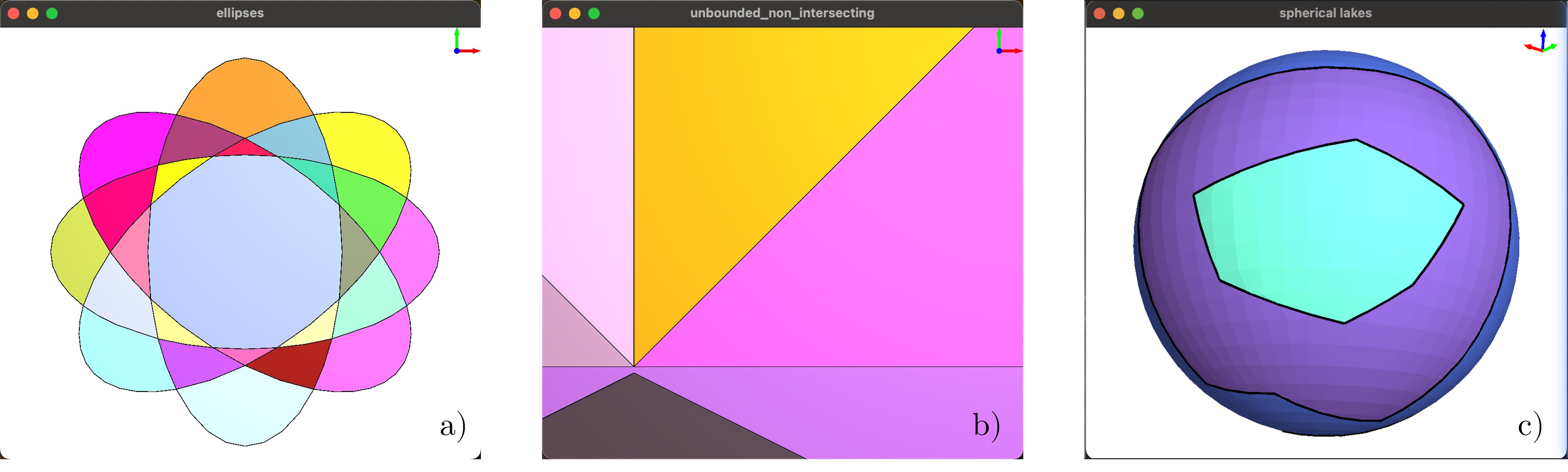1 Arrangements induced by different types of curves. Arrangement faces are rendered with randomized colors: a) several ellipses; b) rays and lines; c) geodesic arcs on unit sphere.

Motivations

The existing draw tool renders arrangements by recursively traversing arrangement faces from the topologically outermost faces inward. For each face it approximates only the outer boundary and forwards the resulting polygon to the Graphics_scene for triangulation and rendering. This approach is straightforward and leverages existing CGAL utilities, but in practice it exposes several limitations that motivated this work:

  1. Rendering Efficiency. Drawing faces with holes by stacking up polygons causes overdraw of pixels. It is often preferable to produce a triangulation of the face domain consisting of non-overlapping triangles even if the primitive count increases.
  2. Lack of support for unbounded curves and faces. The Approximate_2 functor concept used by CGAL::draw() does not accept a bounding box parameter. This prevents correct handling of infinite x-monotone curves (lines, rays) or unbounded faces.
  3. Inability to render faces on curved surfaces. Graphics_scene’s underlying triangulation assumes planar polygonal boundaries. Faces that lie on curved surfaces (e.g. the unit sphere) can’t be automatically handled.

Building on the original draw implementation and the two Aos2 demos, I extended and refined these approaches, addressing the limitations outlined above while reusing existing CGAL components wherever possible. This allowed for efficient, accurate, and flexible rendering of both bounded and unbounded arrangement faces, including those on curved surfaces.

Technical Overview

Reducing Rendering to 2D

The Aos2 package is designed to handle arrangements on parametric surfaces. Since there exists a one-to-one mapping between geometric coordinates on a surface and the two-dimensional parameter space, it is natural to try reducing the processing steps to 2D.

For individual points, the mapping is straightforward: points can be projected into parameter space during processing and then mapped back to the surface before rendering. However, handling curves and faces is more complex. Fortunately, x-monotone curves are not allowed to cross the boundary edges of the parameterized domain. With an appropriate choice of projection, continuity of arrangement curves can be preserved. Arrangement faces, on the other hand, have no such restriction. To address this, we explicitly insert identification curves into the arrangement, making the topology of arrangements on curved surfaces equivalent to a planar arrangement.

This approach introduces unwanted geometric objects and modifies the arrangement instance, which should never happen within a draw function implementation. However, creating a copy of the arrangement (memory overhead is acceptable since most geometric objects are reference-counted) is allowed. By using arrangement observers, we can track modifications during insertion, set up associations between the original features and the split ones, and forward rendering parameters (colors, etc.) calls to the original graphics scene options. As a result, visually equivalent scenes can be produced without any loss of fidelity.

This strategy provides two significant benefits, at the cost of slightly reduced mesh quality:

  • Unified codebase for 2D and 3D cases. Both planar and curved-surface arrangements can be handled with the same pipeline. Large portions of the processing logic are shared, and compile-time dispatching techniques minimize overhead for purely 2D cases.
  • Improved extensibility and efficiency. There is no dependency on specialized triangulation classes for curved surfaces or expensive 3D mesh generation methods.

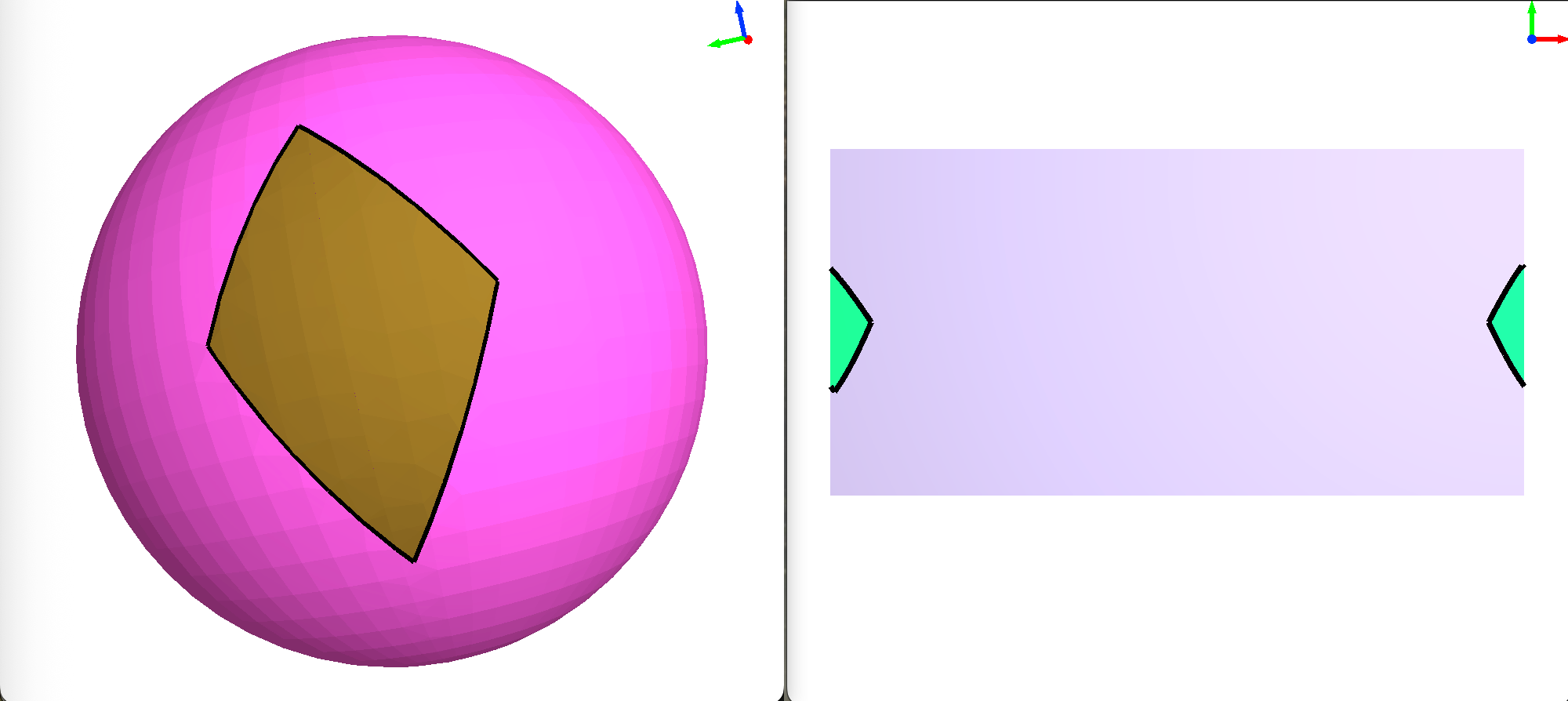image-20250901150126357 Left: Arrangement on the unit sphere with two faces, one spanning across the identification curve. Right: the same arrangement with reverse projection disabled.

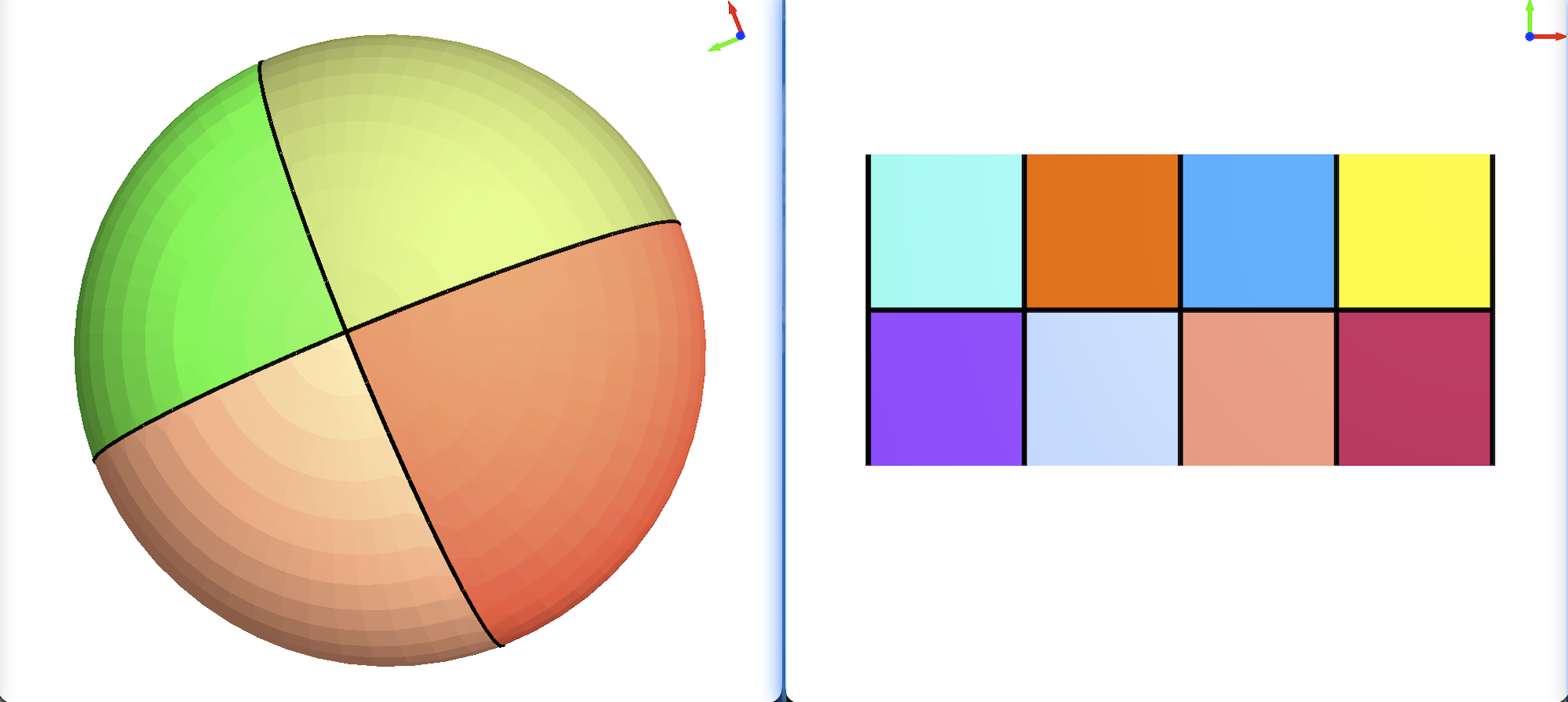image-20250901150413872 Left: Arrangement dividing the sphere into eight equal regions. Right: the same arrangement with reverse projection disabled.

Bounded Curve Approximation

The renderer is designed for on-demand rendering: only arrangement features within a given parameter-space bounding box are approximated and rendered.

Meanwhile, a new concept, AosApproximateUnboundedTraits_2, was introduced to extend curve approximation by taking an additional Bbox_2 parameter, which defines the region of parameter space in which the approximated x-monotone curve segments must lie.

A subtle but important case arises when the bounding box is fully contained within a single arrangement face. In this situation, the curve approximation produces no segments outside the box, which would otherwise leave the face entirely unrendered. To address this, we generate synthetic endpoints at the corners of the bounding box, ensuring that clipped curves are properly represented.

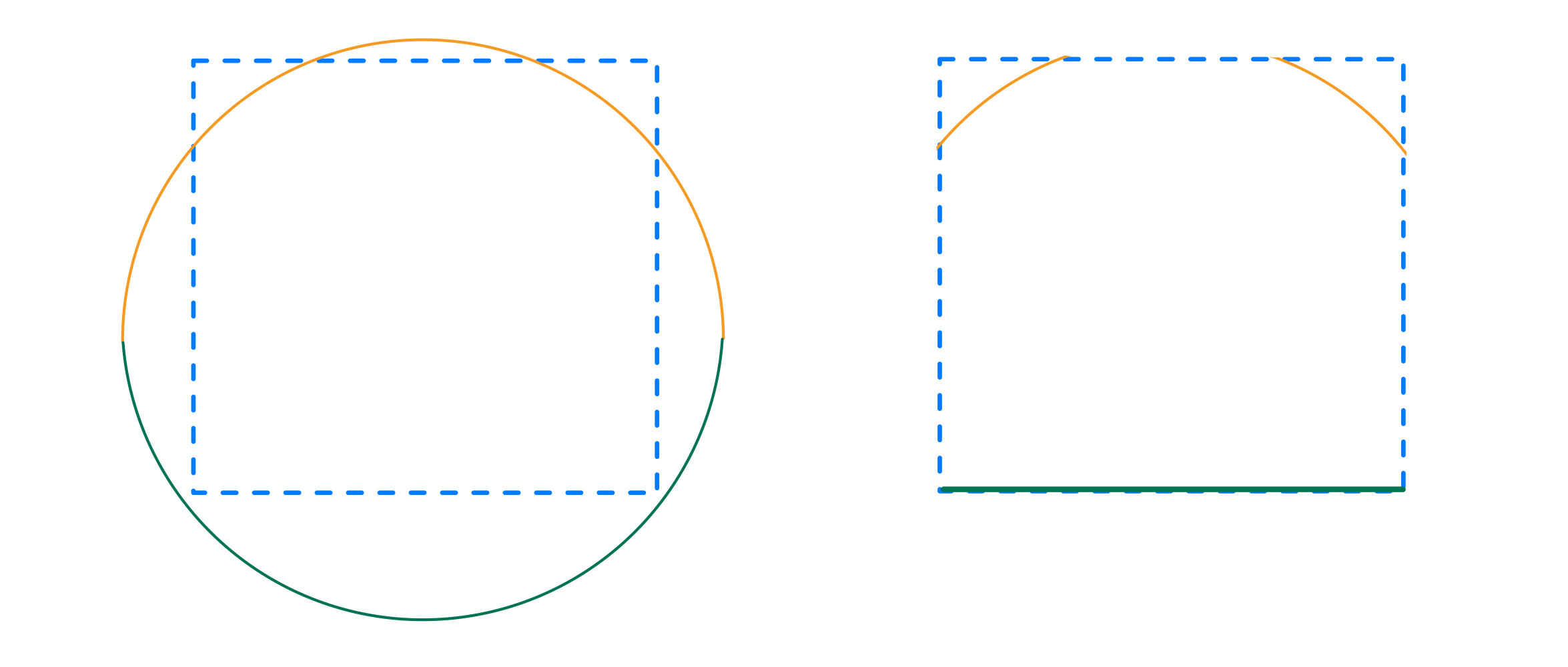Approximation of curves Bounded approximation of two half circles. The bottom curve is horizontally clipped and vertically projected onto the bottom edge of bbox

Customized Face Triangulation

A new class, Arr_bounded_face_triangulator, was introduced to provide finer control over the triangulation process.

For planar arrangements, Constrained_triangulation_2 is sufficient. However, for arrangements on curved surfaces, Constrained_Delaunay_triangulation_2 is required, along with an additional step of inserting pre-generated interior points to ensure high-quality mesh of surface patches. The algorithm used to generate interior points is surface-specific. For example, on spheres we employ UV-grid sampling. The generated points are later assigned to faces using batched point location queries.

In addition, Arr_bounded_face_triangulator handles topological ambiguities caused by bounded rendering. For instance, consider a face defined by nested squares. If the rendering bounding box lies entirely within the inner hole, the approximated curves collapse onto the box edges, making it impossible to distinguish the outer boundary from the inner one. This issue is resolved by inserting dynamically offset midpoints along the bounding box boundary segments, which restores the necessary topological distinction.

Approximating Unbounded Faces

Aos2 handles arrangements of unbounded curves by introducing an implicit bounding rectangle at infinity. On the outer boundary of an arrangement face, several halfedges are marked as fictitious (having no corresponding x-monotone curve). When approximating an unbounded face, this must be taken into account: we detect which side the fictitious halfedge lies on and generate a dummy segment along the corresponding edge of the rendering region, following the direction of the halfedge.

Software Design

Contextual Rendering

Rendering a specific region of an arrangement is a computationally intensive task. To enhance user experience, approximation procedures are executed in a separate thread, rather than mixing them with on-screen painting and GUI event handling. A common pattern for managing concurrent tasks and shared data is to build thread-safe context classes. In this scenario, implementing a full context tree is redundant, so we use a basic cancellable context based on a boolean signal variable. Several mixins are also implemented to conveniently compose geometric predicates, parameterization, and rendering parameters with type safety.

Tiling & Caching

To maintain responsiveness when camera parameters are updated, the class Arr_viewer is derived from Basic_viewer. To maximize cache efficiency, we define a series of discretized approximation error levels and divide the parameter space at each level into rectangular tiles. Each tile is identified by a triple (level, x, y), forming a spatial-partitioning quadtree. We apply the least-recently-used (LRU) caching strategy to handle cache invalidation, ensuring efficient reuse of previously computed tiles.

Showcases

Various arrangements

gaussian_map_tetra

spherical_random

Acknowledgments

I would like to express my sincere gratitude to my mentor, Efi Fogel, for providing guidance, encouragement, and insightful reviews throughout this fantastic GSoC journey.

I am also grateful to the CGAL community for creating such a rich and well-documented library, which made this project possible. Special thanks to the GSoC administrators and organizers for running the program and providing this opportunity for students worldwide to contribute to open-source software.